Effective emissivity of a blackbody cavity depends to a great extent not only on values of emissivity (or reflectance) of cavity walls but also on angular distribution of radiation emitted or reflected by the internal surface of a cavity. Spectral and angular reflection properties of opaque material are described comprehensively by its spectral BRDF (bidirectional reflectance distribution function) introduced by F. E. Nicodemus et al. (1977). Usually, BRDF is considered as a function of five variables (wavelength, two angular coordinates for the incidence direction, and two others for the viewing direction). Integration of the BRDF over hemispherical solid angle gives spectral directional-hemispherical reflectance (DHR). Spectral directional emissivity is equal to 1 minus the spectral DHR, if, according to the optical reciprocity principle, to substitute the direction of incidence for DHR by the direction of observation for directional emissivity. Measurement of BRDF for entire spectral and angular domains of interest is very laborious problem; usually BRDF is measured only for several wavelengths and several incidence angles; often, BRDF is measured only in the plane of incidence (so-called in-plane BRDF). Since the use of measured BRDF in calculations of radiation characteristics of blackbody cavities remains problematic due to incompleteness of experimental data, the reflection models of various degree of adequacy and complexity are employed in radiometric calculations.
Diffuse Reflection Model
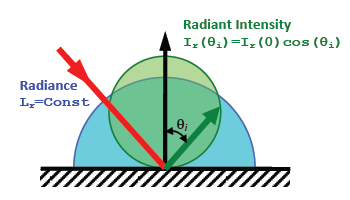
This is the simplest model which considers reflected radiation as perfectly diffuse (Lambertian), that is the radiance intensity of reflected radiation does not depend on the incidence angle and obeys Lambert's cosine law for the viewing angle; the radiance of reflected radiation does not depend on the incidence nor the viewing direction. Diffuse model of reflection allows to write integral equations for effective emissivity in a closed form, accordingly the diffuse model was used in early works on radiation properties of cavity even though its limited applicability to real-world materials.
Uniform Specular-Diffuse (USD) Reflection Model
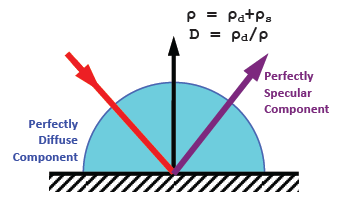
The uniform specular-diffuse (USD) model is in common use in radiative heat transfer theory since 1960ths. USD represents reflected radiation as a sum of perfectly diffuse and perfectly specular components; both components do not depend on the incidence angle. This model is completely determined by the DHR ρ and the diffusity D. The USD model includes the Diffuse model as a special case. The USD model is simple to understand and for results interpreting; it is well-suited for Monte Carlo modeling of radiation heat transfer. Blackbody emissivity modeling programs STEEP321 and PyramidA employ the USD model. Its special case of wavelength-independent reflectance referred to as the Gray Uniform Specular-Diffuse (Gray USD) model is used in STEEP320 program.
The inherent drawbacks of the USD model are (i) impossibility to fit it to measured data because the BRDF of the perfectly specular component is the Dirac delta-function that has infinite value in the direction of specular reflection, (ii) an ambiguity in separation of measured DHR onto diffuse and specular parts, and (iii) ignoring the dependence of reflectance on the incidence angle. Therefore, the USD model cannot predict some fine effects which are determined by the angular distribution of reflected radiation.
Three-Component (3C) BRDF Model
The 3C BRDF model was introduced by A. Prokhorov, 2012a. The model represents BRDF of a material as a weighted sum of three independent components: diffuse (Lambertian), glossy, and quasi-specular, i.e., having a specular lobe of small but finite width. The 3C BRDF model has 8 parameters which can be fitted to the measured in-plane BRDFs. By supposing that proportion of components remains the same within some spectral range, one can split the spectral DHR measured at one incidence angle onto diffuse, glossy, and quasi-specular components (see A. Prokhorov, 2012b).
This is the simplest model which considers reflected radiation as perfectly diffuse (Lambertian), that is the radiance intensity of reflected radiation does not depend on the incidence angle and obeys Lambert's cosine law for the viewing angle; the radiance of reflected radiation does not depend on the incidence nor the viewing direction. Diffuse model of reflection allows to write integral equations for effective emissivity in a closed form, accordingly the diffuse model was used in early works on radiation properties of cavity even though its limited applicability to real-world materials.
Uniform Specular-Diffuse (USD) Reflection Model
The uniform specular-diffuse (USD) model is in common use in radiative heat transfer theory since 1960ths. USD represents reflected radiation as a sum of perfectly diffuse and perfectly specular components; both components do not depend on the incidence angle. This model is completely determined by the DHR ρ and the diffusity D. The USD model includes the Diffuse model as a special case. The USD model is simple to understand and for results interpreting; it is well-suited for Monte Carlo modeling of radiation heat transfer. Blackbody emissivity modeling programs STEEP321 and PyramidA employ the USD model. Its special case of wavelength-independent reflectance referred to as the Gray Uniform Specular-Diffuse (Gray USD) model is used in STEEP320 program.
The inherent drawbacks of the USD model are (i) impossibility to fit it to measured data because the BRDF of the perfectly specular component is the Dirac delta-function that has infinite value in the direction of specular reflection, (ii) an ambiguity in separation of measured DHR onto diffuse and specular parts, and (iii) ignoring the dependence of reflectance on the incidence angle. Therefore, the USD model cannot predict some fine effects which are determined by the angular distribution of reflected radiation.
Three-Component (3C) BRDF Model
The 3C BRDF model was introduced by A. Prokhorov, 2012a. The model represents BRDF of a material as a weighted sum of three independent components: diffuse (Lambertian), glossy, and quasi-specular, i.e., having a specular lobe of small but finite width. The 3C BRDF model has 8 parameters which can be fitted to the measured in-plane BRDFs. By supposing that proportion of components remains the same within some spectral range, one can split the spectral DHR measured at one incidence angle onto diffuse, glossy, and quasi-specular components (see A. Prokhorov, 2012b).
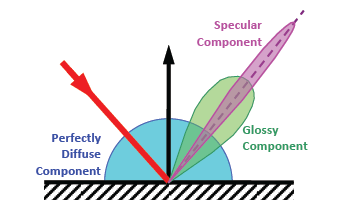

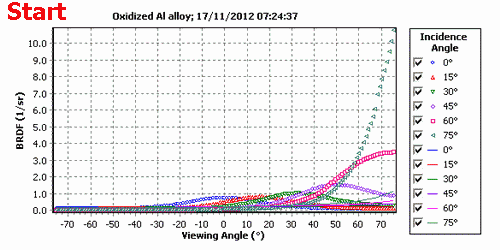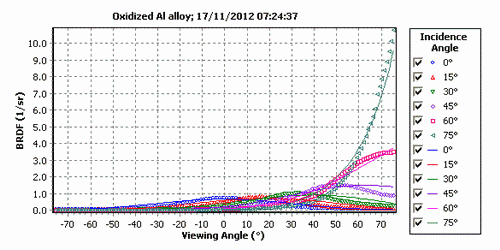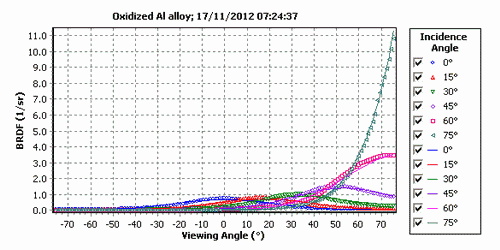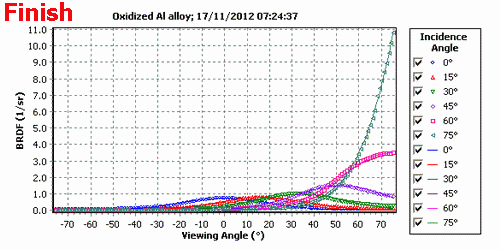
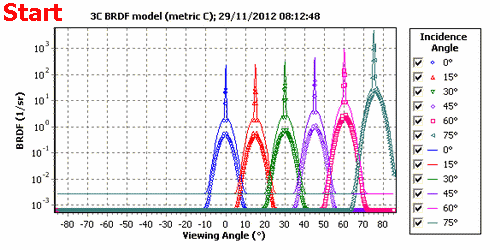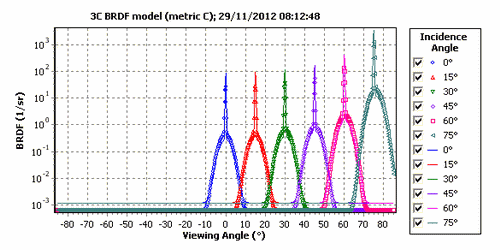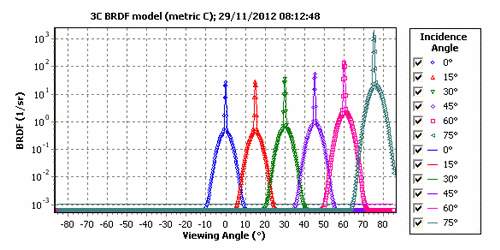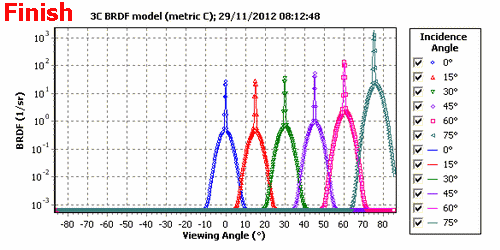
The 3C BRDF model includes the Diffuse Model as a special case but the USD model cannot be reproduced by the 3C model due to inherent dependence of the quasi-specular term on the incidence angle.
Virial International implemented the algorithm of Particle Swarm Optimization method for fitting parameters of the 3C model to the measured monochromatic in-plane BRDF and the procedure of spectral DHR splitting into STEEP323 and INCA333 blackbody modeling programs.
Virial International implemented the algorithm of Particle Swarm Optimization method for fitting parameters of the 3C model to the measured monochromatic in-plane BRDF and the procedure of spectral DHR splitting into STEEP323 and INCA333 blackbody modeling programs.
These two simple animations demonstrate convegence of the fitting process for the near-diffuse (on the left) and the near-specular (on the right) materials.

