

Satori111 is intended for calculation of parameters in the Sakuma-Hattori interpolation equation and can be used at radiometric temperature calibration of radiation thermometers (pyrometers) and blackbody radiation sources by multiple-point method.
Download Satori111 Evaluation Version (1.4 MB)
Download Satori111 Manual (1.8 MB)
Click here to buy
Download Satori111 Evaluation Version (1.4 MB)
Download Satori111 Manual (1.8 MB)
Click here to buy
Satori111 allows fitting the Sakuma-Hattori equation for up to 20 reference temperatures from 100 to 4000 K both for narrow-band and wide-band radiation thermometers. After determination of the Sakuma-Hattori parameters, up to 1000 signals of the radiation thermometer can be converted into temperatures at once.
Satori111 stores the initial data and calculation results in built-in expandable database and represents them in the spreadsheet and graphical form. All graphs are customizable and editable. Data can be copied into the clipboard, exported as text (ASCII), XLS, XML, and HTML table; graphs can be copied into the clipboard, saved as bitmap or Windows metafile, and printed out.
Satori111 computes the Sakuma-Hattori parameters using the Levenberg-Marquardt method then verifies them by the Particle Swarm Optimization.
The animation on the right displays in real time the process of verification by the Particle Swarm Optimization. The blue squares are for solutions obtained by the Levenberg-Marquardt method, the red crosses are for Particle Swarm Optimization.
Satori111 stores the initial data and calculation results in built-in expandable database and represents them in the spreadsheet and graphical form. All graphs are customizable and editable. Data can be copied into the clipboard, exported as text (ASCII), XLS, XML, and HTML table; graphs can be copied into the clipboard, saved as bitmap or Windows metafile, and printed out.
Satori111 computes the Sakuma-Hattori parameters using the Levenberg-Marquardt method then verifies them by the Particle Swarm Optimization.
The animation on the right displays in real time the process of verification by the Particle Swarm Optimization. The blue squares are for solutions obtained by the Levenberg-Marquardt method, the red crosses are for Particle Swarm Optimization.


Minimal requirements to hardware and software:
Processor frequency 1 GHz
RAM 3 GB
Hard disk space 10 MB
Operation system Windows XP and 7 (32 and 64-bit), Windows 8 in Compatibility Mode
Processor frequency 1 GHz
RAM 3 GB
Hard disk space 10 MB
Operation system Windows XP and 7 (32 and 64-bit), Windows 8 in Compatibility Mode
where c2 = 1.4387770123·10-2 m K is the 2nd radiation constant in the Plank law, A, B, and C are adjustable constants (curve-fitting parameters).
The inverse Sakuma-Hattori equation
allows to compute temperature T if the signal S of a radiation thermometer is measured and Sakuma-Hattori parameters A, B, and C and are found from measurements conducted for at least 3 temperature of a blackbody.
When the number of reference temperatures (e. g., fixed points of the ITS-90 temperature scale) n>3, the Sakuma-Hattori parameters can be found using the least square approach. Mathematically, this task is equivalent to the minimization problem for the objective function
When the number of reference temperatures (e. g., fixed points of the ITS-90 temperature scale) n>3, the Sakuma-Hattori parameters can be found using the least square approach. Mathematically, this task is equivalent to the minimization problem for the objective function
where Si are signals for n reading of a radiation thermometer aimed at a blackbody with temperatures Ti, i = 3,...,n.
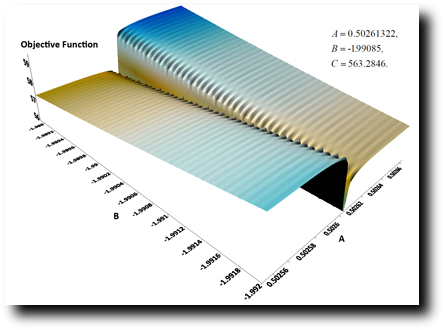
The objective function χ has local minima and complicated shape (see two-dimensional plots below) what makes the fitting of the Sakuma-Hattori parameters to experimetal data a non-trivial problem.
The objective function χ has local minima and complicated shape (see two-dimensional plots below) what makes the fitting of the Sakuma-Hattori parameters to experimetal data a non-trivial problem.


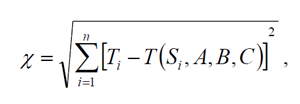
2D slice of the Objective Function for high-temperature reference points and narrow-band pyrometer with the mean wavelength of 0.5 µm.
2D slice of the Objective Function for 4 ITS-90 fixed points and wide-band radiation thermometer with the mean wavelength of 10.6 µm.
The Sakuma-Hattori equation (F. Sakuma and S. Hattori, “Establishing a Practical Temperature Standard by Using a Narrow-Band Radiation Thermometer with a Silicon Detector,” in Temperature: Its Measurement and Control in Science and Industry, ed. by J. F. Schooley, AIP, New York, Vol. 5, pp. 421-427 (1982)) expresses the signal of the radiation thermometer as a function of blackbody temperature:
Satori111 employs the Levenberg-Marquardt algorithm to find the calibration coefficients A, B, and C and the Particle Swarm Optimization - stochastic method of global optimization - to avoid wrong solutions corresponding to the local minima and, in such a way, verify the results.

