The temperature distribution over the surface of a blackbody radiator is one of the most crucial factors determining the radiation characteristics of a blackbody. High-quality blackbody radiator must be almost isothermal. Fixed-point and heat-pipe blackbodies as well as cavities immersed into thermostated liquid have the highest degree of temparature uniformity. However, real-world cavities are always nonisothermal. Even if the external surface of a cavity has ideally uniform temperature, the finite thermal resistance of a cavity wall (or layers forming it) and different radiative heat losses through the aperture for different parts of the cavity internal surface unavoidably lead to temperature non-uniformity of radiating surface. Evaluation of this effect is possible by computational methods.
Temperature non-uniformity of radiating surface affects significantly the effective emissivity of a blackbody, escpecially if the area within the field-of-view of the detector, radiometer, or radiation thermometer is nonisothermal. Non-uniformity of radiating surface leads to different contributions of radiation emitted by cavity wall different elements into the resulting cavity radiation. This, in turn, makes the cavity spectrum non-Planckian.
Effective emissivity is the ratio of a radiometric quantity (usually, radiance or spectral radiance) of a blackbody radiator at a certain temperature to the same quantity of a perfect BB with the same temperature. To avoid ambiguity in temperature assigned to the perfect blackbody in the effective emissivity definition, the reference temperature Tref has to be introduced and assigned to the perfect BB. Tref itself has no specific physical meaning; its choice, in general, is arbitrary. Depending on the choice, the spectral effective emissivity of a nonisothermal blackbody can take any positive value, i.e., be greater than one. Spectral radiances of a blackbody do not change their values at any choice of Tref. In practice, the temperature measured by a contact temperature sensor is commonly used as Tref to keep effective emissivities of the nonisothermal blackbody comparable with those for the isothermal case. Effective emissivity of a nonisothermal cavity depends on the wavelength even if the cavity internal surface has wavelength-independent optical characteristics.
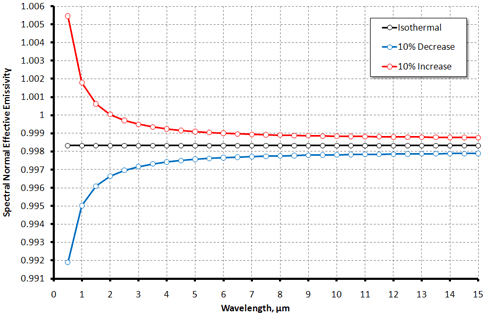
For exemplification of this phenomenon, the dependences of the normal spectral effective emissivity on wavelength for gray diffuse cylindrical cavity having wall emissivity of 0.9 are shown below. Cavty bottom is isothermal at 1300 K; three temperature distributions are considered: (Isothermal) all cavity walls have uniform temperature of 1300 K; 10% Decrease: linear decrease of temperature along cylindrical surface from 1300 K down to 1287 K, the diaphragm has the uniform temperature of 1287 K; 10% Increase: linear increase of temperature along cylindrical surface from 1300 K up to 1313 K, the diaphragm has the uniform temperature of 1313 K. In all cases, Tref = 1300 K.
Temperature non-uniformity of radiating surface affects significantly the effective emissivity of a blackbody, escpecially if the area within the field-of-view of the detector, radiometer, or radiation thermometer is nonisothermal. Non-uniformity of radiating surface leads to different contributions of radiation emitted by cavity wall different elements into the resulting cavity radiation. This, in turn, makes the cavity spectrum non-Planckian.
Effective emissivity is the ratio of a radiometric quantity (usually, radiance or spectral radiance) of a blackbody radiator at a certain temperature to the same quantity of a perfect BB with the same temperature. To avoid ambiguity in temperature assigned to the perfect blackbody in the effective emissivity definition, the reference temperature Tref has to be introduced and assigned to the perfect BB. Tref itself has no specific physical meaning; its choice, in general, is arbitrary. Depending on the choice, the spectral effective emissivity of a nonisothermal blackbody can take any positive value, i.e., be greater than one. Spectral radiances of a blackbody do not change their values at any choice of Tref. In practice, the temperature measured by a contact temperature sensor is commonly used as Tref to keep effective emissivities of the nonisothermal blackbody comparable with those for the isothermal case. Effective emissivity of a nonisothermal cavity depends on the wavelength even if the cavity internal surface has wavelength-independent optical characteristics.
For exemplification of this phenomenon, the dependences of the normal spectral effective emissivity on wavelength for gray diffuse cylindrical cavity having wall emissivity of 0.9 are shown below. Cavty bottom is isothermal at 1300 K; three temperature distributions are considered: (Isothermal) all cavity walls have uniform temperature of 1300 K; 10% Decrease: linear decrease of temperature along cylindrical surface from 1300 K down to 1287 K, the diaphragm has the uniform temperature of 1287 K; 10% Increase: linear increase of temperature along cylindrical surface from 1300 K up to 1313 K, the diaphragm has the uniform temperature of 1313 K. In all cases, Tref = 1300 K.
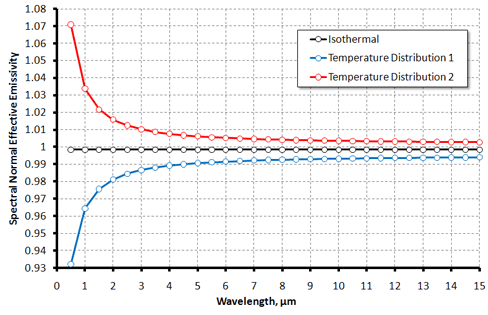
Temperature nonuniformity of the area of cavity's internal surface within field-of-view (that is directly "viewed" by measuring device) results in drastic changes of spectral effective emissivity. In the right-hand graph, the spectral effective emissivity is plotted against wavelength for the same cavity as in previous example and two following temperature distribution:
Temperature distribution 1: temperature linearly decreases from 1300 K at the bottom center down to 1290 K at its periphey, then decreases linearly along cylindrical wall down to 1287 K; cavity diaphragm has constant temperature of 1287 K.
Temperature distribution 2: Temperature linearly increases from 1300 K at the bottom center up to 1310 K at its periphey, then increases linearly along cylindrical wall up to 1313 K; cavity diaphragm has constant temperature of 1313 K. Tref equals to 1300 K for all cases.
Temperature distribution 1: temperature linearly decreases from 1300 K at the bottom center down to 1290 K at its periphey, then decreases linearly along cylindrical wall down to 1287 K; cavity diaphragm has constant temperature of 1287 K.
Temperature distribution 2: Temperature linearly increases from 1300 K at the bottom center up to 1310 K at its periphey, then increases linearly along cylindrical wall up to 1313 K; cavity diaphragm has constant temperature of 1313 K. Tref equals to 1300 K for all cases.
Effective emissivity of an isothermal cavity doesn't depend on the cavity temperature only if cavity is surrounded by the non-emitting media (i.e., vacuum at 0 K), or if the background influence is negligible. Since the actual characteristics of background radiation is very seldom known, usually, one can consider cavity's surroundings as a perfect blackbody radiator with the "background temperature" Tbg.
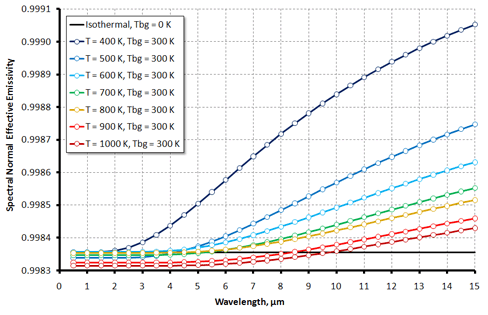
The influence of Tbg = 300 K on the spectral normal effective emissivities of the above-mentioned cavity having isothermal walls at T = Tref = 400...1000 K is shown at left. Black line corresponds to the case of the isothermal cavity at Tbg = 0 K.
The radiance temperature measured in conditions of non-zero background will differ from the termodynamic temperature of a cavity not only due to deviation of the effective emissivity from unity but also due to contribution of the background radiation partially reflected by the cavity.
The influence of Tbg = 300 K on the spectral normal effective emissivities of the above-mentioned cavity having isothermal walls at T = Tref = 400...1000 K is shown at left. Black line corresponds to the case of the isothermal cavity at Tbg = 0 K.
The radiance temperature measured in conditions of non-zero background will differ from the termodynamic temperature of a cavity not only due to deviation of the effective emissivity from unity but also due to contribution of the background radiation partially reflected by the cavity.
For nonisothermal cavities, both effects (temperature non-uniformity and radiating background) act conjointly. Moreover, temperature effects cannot be considered in isolation from the optical properties of the cavity walls. In terms of the Monte Carlo ray tracing, during multiple reflections, a ray "accumulates" spectral radiances at temperatures of all reflection points. For different angular distributions of reflected radiation, these points will be distributed differently over the cavity surface, therefore, their contribution will be also different.
Programs STEEP320, STEEP321, and STEEP323 allow modeling axially-symmetric temperature distributions along cavity generatrix. Temperatures can be defined over the discrete point set; linear interpolation is used during ray tracing.
INCA333 allows to model one-dimensional temperature distributions along the axis of the cavity cylindrical part; the diaphragm is supposed to be isothermal at the temperature of the adjacent edge of the cylindrical part.
PyramidA uses linear interpolation between temperature of the top of pyramids and the base of the pyramid array. It is supposed that the base has uniform temperature.
As a part of existing software customization service, Virial International offers modification of methods for input and interpolation of temperatures to satisfy various customer requirements.
Programs STEEP320, STEEP321, and STEEP323 allow modeling axially-symmetric temperature distributions along cavity generatrix. Temperatures can be defined over the discrete point set; linear interpolation is used during ray tracing.
INCA333 allows to model one-dimensional temperature distributions along the axis of the cavity cylindrical part; the diaphragm is supposed to be isothermal at the temperature of the adjacent edge of the cylindrical part.
PyramidA uses linear interpolation between temperature of the top of pyramids and the base of the pyramid array. It is supposed that the base has uniform temperature.
As a part of existing software customization service, Virial International offers modification of methods for input and interpolation of temperatures to satisfy various customer requirements.