Direct measurements of effective emissivity of blackbody radiation sources are often extremely difficult or even impossible. Sometimes, computational methods are the only way to determine effective emissivity. Moreover, calculation of effective emissivities should be done at the design stage. Many computational methods for effective emissivities have been developed since 1950ths. These methods are based on the various physical and mathematical assumptions, have different areas of applicability and provide different degrees of accuracy. At present, the most comprehensive and flexible method for calculating radiation characteristics of blackbody radiators is the Monte Carlo method. It is based on the ray tracing algorithm that models radiation heat exchange among cavity walls and propagation of radiation from a blackbody to a radiation detector. The Monte Carlo method uses the ray (geometrical) optics approximation; such phenomena as polarization and diffraction are not considered.
The Monte Carlo algorithms employed in Virials's blackbody emissivity modeling software is based on the optical reciprocity principle and the technique of backward ray tracing. The history of a ray directed from the point of observation into a cavity is being traced until it leaves the cavity after reflections from the cavity walls, or until its energy becomes less then the given value (flux threshold). The last point of reflection is considered as a birth point of a ray propagating in opposite direction. The spectral radiance acquired by a ray consists of the spectral radiance in the viewing direction of the thermal radiation computed by Plancks law for the last reflection point and the sum of spectral radiances in the points of successive reflectance computed along the ray trajectory and impaired by multiple reflections. Averaging of spectral radiances of a large number of rays allows to estimate the effective emissivity and other radiation characteristics of a cavity.
Precision of the Monte Carlo calculations is in inverse proportion to the square root of a number of rays traced; usually, it is enough to trace from 105 to 107 rays to achieve the accuracy of 10-4
10-6 in effective emissivity.
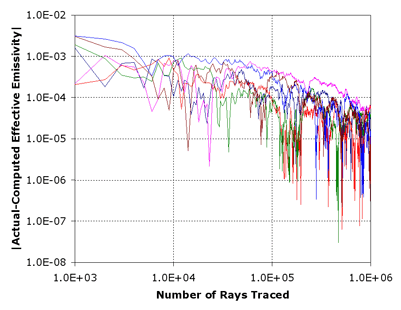
The logarithmic plot to the right illustrates the stochastic convergence of the Monte Carlo modeling for several calculation processes performed for a diffuse spherical cavity, for which the effective emissivity can be calculated exactly, using well-known analytical formula.
Monte Carlo calculation can be considered as a numerical experiment similar to the ordinary natural experiment. Therefore, its accuracy can be assessed by performing repeated calculations and statistical processing of results.
Adequacy of the Monte Carlo modeling depends equally to a great extent upon two factors. The first is the temperature distribution over the blackbody internal surface, especially over their directly viewable areas. One can evaluate the effect of temperature non-uniformity on the radiation characteristics of a blackbody by performing calculations with several feasible temperature distributions.
The logarithmic plot to the right illustrates the stochastic convergence of the Monte Carlo modeling for several calculation processes performed for a diffuse spherical cavity, for which the effective emissivity can be calculated exactly, using well-known analytical formula.
Monte Carlo calculation can be considered as a numerical experiment similar to the ordinary natural experiment. Therefore, its accuracy can be assessed by performing repeated calculations and statistical processing of results.
Adequacy of the Monte Carlo modeling depends equally to a great extent upon two factors. The first is the temperature distribution over the blackbody internal surface, especially over their directly viewable areas. One can evaluate the effect of temperature non-uniformity on the radiation characteristics of a blackbody by performing calculations with several feasible temperature distributions.
Second factor crucially affected effective emissivity is the adequacy of angular dependences of the model adopted for optical properties of materials forming the blackbody. Click here to learn more about reflection models.
Further reading:
J. R. Howell, R. D. Siegel, and M. P. Mengüç, "Thermal Radiation Heat Transfer," 5th Ed., CRC Press, 2010 - 10-5. The Monte Carlo Method
E. M. Sparrow and R. D. Cess, "Radiation Heat Transfer," Augmented Ed., Hemisphere, 1978 - 5-4. The Monte Carlo Method
J. R. Mahan, "Radiation Heat Transfer: A Statistical Approach," Wiley, 2002
A. V. Prokhorov, "Monte Carlo method in optical radiometry," Metrologia 35, 465-471 (1998)
V. I. Sapritsky and A. V. Prokhorov, "Spectral effective emissivities of nonisothermal cavities calculated by the Monte Carlo method,"
Appl. Opt. 34, 5645-5652 (1995)
V. I. Sapritsky and A. V. Prokhorov, "Calculation of the effective emissivities of specular-diffuse cavities by the Monte Carlo method,"
Metrologia 29, 9-14 (1992)
Further reading:
J. R. Howell, R. D. Siegel, and M. P. Mengüç, "Thermal Radiation Heat Transfer," 5th Ed., CRC Press, 2010 - 10-5. The Monte Carlo Method
E. M. Sparrow and R. D. Cess, "Radiation Heat Transfer," Augmented Ed., Hemisphere, 1978 - 5-4. The Monte Carlo Method
J. R. Mahan, "Radiation Heat Transfer: A Statistical Approach," Wiley, 2002
A. V. Prokhorov, "Monte Carlo method in optical radiometry," Metrologia 35, 465-471 (1998)
V. I. Sapritsky and A. V. Prokhorov, "Spectral effective emissivities of nonisothermal cavities calculated by the Monte Carlo method,"
Appl. Opt. 34, 5645-5652 (1995)
V. I. Sapritsky and A. V. Prokhorov, "Calculation of the effective emissivities of specular-diffuse cavities by the Monte Carlo method,"
Metrologia 29, 9-14 (1992)



